Edge Coloring Complete Graphs of Even Order
31 December 2020Recently, I rediscovered a special case of Baranyani's Theorem. Specifically, that of @@r=2@@, a result which has apparently been known since the 1800s. It states that every complete graph with an even number of vertices @@n@@ has a proper edge coloring with @@n-1@@ colors. Alternatively, it is possible to partition the edges of @@K_n@@ into @@n-1@@ sets (colors) such that no two edges in the same set share an endpoint. Clearly, this is the least possible number of colors — each vertex has @@n-1@@ edges going out of it. The theorem states that, for even @@n@@, it is possible to attain this minimum.
I actually discovered this fact in a context completely separate from graph theory. This semester, I served as a TA for CS 2110 at Georgia Tech. It was fun, though time consuming, and I thought a lot about how to best teach struggling students. I remembered that pair programming is a common technique used to guide new developers, but it could never be implemented in the course. Nonetheless, I went on a tangent thinking about how one could implement pair programming in a class. Ideally, the same students wouldn't work together all the time — usually the teacher would mix them around. How long it would take before we're forced to repeat, and a student is paired with someone they've already worked with?
I assumed the number of students @@n@@ was even for simplicity. Each day, we take @@\frac{1}{2}n@@ subsets of size two, making sure none of them share an element. We also want to never repeat subsets. In that case, the longest we can possibly sustain this process is clearly
%% \frac{\text{# Total Subsets}}{\text{# Subsets per Day}} = \frac{\binom{n}{2}}{\frac{1}{2}n} = n-1 %%
days. I still had to show we can't be cut short, though, and that's what I set out to do.
I started as I usually do, taking small examples and trying to find some pattern. One of the first things I noticed was that a greedy algorithm wouldn't always work. In the case above, for example, a greedy approach fails on the second day (row). After taking @@\{1,3\}@@, the algorithm takes @@\{2,4\}@@ then is forced to repeat @@\{5,6\}@@. There might've been some ordering with which this approach would work, and we see later that this is the case, but I decided to look elsewhere.
Another pattern I noticed had to do with the first and last lines in the arrangement above. It's not immediately obvious from the figure, so consider the "re-arrangement" below.
%% \begin{align*} \{1,2\} \, \{3,4\} \, \{5,6\} \nl \{2,3\} \, \{4,5\} \, \{1,6\} \end{align*} %%
The first row contains subsets of adjacent numbers starting at @@1@@ and going up. The same is true for the last row, except it starts at @@2@@ (and wraps around). Another way see this configuration is to start by taking the sets with adjacent elements in the "natural" order — @@\{1,2\}@@, @@\{2,3\}@@, all the way up to @@\{6,1\}@@ — then to place all these sets, alternating days as we go. This was a nice observation, but I couldn't immediately elaborate on it. I would later use it in a different form.
Most of my effort focused on looking for some recursive pattern — some way to create the case of @@n+2@@ from that of @@n@@. Initially, the problem would seem to lend itself to induction. The structure above, with the subsets @@\{1,x\}@@ along the right side, looked convenient to work with, and I tried inducting with that. I put the sets @@\{1,2\}@@ along the first @@n-3@@ rows, then worked to "swap" the @@2@@ with some other number (in another set), using the remaining @@2@@ rows to put the "destroyed" sets in. I spent a lot of time here, but never quite got it to work.
That's not to say I didn't make progress, though. One effective way I found to think about this problem was to imagine each pair of students as a permutation, specifically a two-cycle. Each day (row) is then a product of two-cycles, and we're given the constraint that each column must be a permutation as well. This reframing gives a nice table, which I find easier to think about.
An observation I made soon after was the existence of "three-cycles". In the example above, we have the two-cycle @@\begin{pmatrix}1&2\end{pmatrix}@@ on day one, and @@\begin{pmatrix}1&3\end{pmatrix}@@ on day two. This implies that @@\begin{pmatrix}2&3\end{pmatrix}@@ cannot be on days one or two, and must be on some other day (five in this case). I thought this could be made into some algorithm to arrange the cycles with. But, I gave up on it after realizing how much overlap there would be between different three-cycles. Again, I would see this observation later in a different form.
Another observation arising from this framing, and one which I found quite powerful, was the idea of "pointing". For example, in the above arrangement, the @@1@@ on the first day is paired with @@2@@ — the first column of the first row has a @@2@@. So it can be seen as pointing to the @@2@@ (the second column) on the second day. Similarly, the @@2@@ on the second day points to the @@5@@ on the third day, and so on until we cycle back to the first day. Repeatedly following these pointers gives "paths", @@(1,2,5,3,6,1)@@ in this case. This path is "bad" since it repeats a number. "Good" paths are aptly named since the recursive construction from the last section, the one involving @@\{1,x\}@@ sets, can made to work with it. (More on this later.)
In the day-ordering given above, there is no good path starting with any of the numbers. The days can be reordered to give favorable results, though. Nonetheless, I couldn't prove that good orderings always exist, and in fact they don't. While writing this post, I found that the configuration given above is a counterexample. I know this because I wrote some code to check all possible permutations of the days and starting locations.
I also tried shoe-horning new days into old ones, integrating into existing paths regardless of whether they were good or bad, but I didn't make much headway there either.
No, the real breakthrough came when I was studying for MATH 3012. A major part of the course was graph theory. My notes on it were the longest out of all the units, with an entire page devoted to definitions. Most of them were straightforward, but I found the definition for edges peculiar. We defined an edge as a subset of size two of the vertex set, at least in the simple and undirected case.
I had the insight to model each pair of students as an edge in a graph. Then, I'd have to show that @@K_n@@ can be edge-colored with @@n-1@@ colors (for @@n@@ even). The different colors correspond to different days, and forcing the minimum possible number of colors ensures noone is left out on any day — we need all @@\frac{1}{2}n@@ possible edges per color to meet the chromatic number requirement.
The first thing I did was check if something like this was already known, which of course it was. I chose not to look at the proof, though. I wanted to find it myself.
In retrospect, it should've been obvious that I was dealing with a graph problem. The pattern I noticed with "adjacent subsets" — @@\{1,2\}@@, then @@\{2,3\}@@, all the way up to @@\{6,1\}@@ — is simply that even cycles can be two-colored. Specifically, I was looking at the cycle on the "rim" of @@K_n@@, shown below. Similarly, the pattern I noticed with three-cycles is just that triangles have chromatic number @@3@@.
Moreover, my idea with pointers is fundamentally a statement about graphs. A good path is just a path in @@K_n@@ that traverses each of the @@n-1@@ colors exactly once. Graphs with such a path can be used to (recursively) create an edge-coloring for @@K_{n+2}@@ with @@(n+2)-1@@ colors. How?
First note that recoloring some of the old edges in @@K_n@@ with the two new colors won't break its proper coloring, at least not inherently. As long as none of the new colors' edges share a vertex, the resulting coloring will be proper. Phrased differently, the only way to break a proper coloring by recoloring edges is through the edges recolored.
With that in mind, we can take the good path @@P=(x_1,x_2,\cdots,x_n)@@ and integrate it with the two new vertices @@u@@ and @@v@@. Consider the cycle starting at @@u@@, then following the good path @@P@@, then ending at @@v@@ before cycling back. We'll color that even cycle with the two new colors @@c_n@@ and @@c_{n+1}@@. Without loss of generality, let the edges @@\{u,x_1\}@@ and @@\{x_n,v\}@@ be colored with @@c_n@@. As for all the other new edges, color @@\{u,x_i\}@@ the same color that @@\{x_{i-1},x_i\}@@ was before it was overwritten, and similarly color @@\{x_i,v\}@@ whatever @@\{x_i,x_{i+1}\}@@ was. The diagram below might be helpful.
Sadly, recursing in this way doesn't guarantee the existence of a good path in the resulting graph. Like before, I made some effort to use this argument even in the absence of good paths, but I didn't have much luck.
While working on that, I made some other observations that would be important. But before that, I'd like to define some terms.
A day is a set of @@\frac{1}{2}n@@ edges in @@K_n@@ not sharing any vertices.
I devoted a lot of time to finding days. Why? A coloring we're searching for can be seen as a collection of @@n-1@@ different days that don't share any edges. These days would encompass all @@\binom{n}{2}@@ possible edges, and thus provide an @@n-1@@ edge coloring, with each day corresponding to a color. As a sidenote, this term was borrowed from the original problem I was working on.
The length of an edge is the distance between its two endpoints, only going along the rim of the graph.
I found this to be a useful notion. Often, it was helpful to consider only edges between vertices an even or an odd number apart, especially when thinking of the vertices as elements of @@(\mathbb{Z}/n\mathbb{Z})^+@@. (More on that later.) I also found it useful to give special treatment to midlines — edges of length @@\frac{1}{2}n@@, particularly when thinking geometrically. Of course, it has drawbacks. Edge length only makes sense when considering @@K_n@@ drawn out as a regular polygon. The lengths @@\ell@@ and @@n-\ell@@ are the same since it fundamentally works modulo @@n@@. But, I found the notion helpful despite its caveats.
As for my observations, I first noticed that, for odd multiples of two, it's possible to make days with a nice geometric structure. We can take a midline and all the edges perpendicular to it to be in the same day. This one arrangement generates @@\frac{1}{2}n@@ different days through @@180^\circ@@ rotational symmetry, and encompasses all midlines and edges of even length. However, this construction doesn't work when @@n@@ is an even multiple of two since it contains two midlines instead of just one, leading to double counting. I tried to make a similar construction for that case, sometimes trying to recurse down by two as before, but to no avail.
Thankfully, I later noticed that I didn't need to worry about the even multiples of two. Why? In that case, we can see @@K_n@@ as two different complete @@K_{\frac{n}{2}}@@ graphs with vertices connected by a bipartite complete graph @@K_{\frac{n}{2},\frac{n}{2}}@@. It's straightforward to edge-color the latter with @@\frac{1}{2}n@@ colors. Moreover, since @@\frac{1}{2}n@@ is even by assumption, we can recursively color the two @@K_{\frac{n}{2}}@@s with the colors that remain.
Now, I was just left with coloring the edges of odd length, and this is where I got stuck. I couldn't find a geometric way to color them for odd multiples of two. For even multiples, I could take all the edges parallel to a given edge on the rim, but I'd already decided to handle that case with recursion. Trying that same strategy with odd multiples double counted midlines.
Separately from my geometric arguments, I had tried looking at the graph through the lens of "number theory". Numbering all the vertices counterclockwise (or clockwise) starting at zero gives something akin to @@\mathbb{Z}/n\mathbb{Z}@@. I looked at cycles in that ring generated by multiplication and addition. Multiplication wasn't that useful since it left out zero, but addition was. In particular, I noticed that by fixing an odd number @@\ell@@, I could color all edges of length @@\ell@@ with just two colors. Why? Since @@n@@ is even but @@\ell@@ is odd, the cycle @@\langle\ell\rangle@@ generated by @@\ell@@ will have an even number of elements, and even cycles can be two colored. Note that @@\langle\ell\rangle@@ may have multiple cosets, but they're all disjoint, so their edges can reuse the same two colors.
This essentially solved my problem of coloring edges of odd length. There are only @@\frac{1}{4}n-\frac{1}{2}@@ possible values @@\ell@@ can take. We'll thus use @@\frac{1}{2}n-1@@ colors for the edges of odd length, plus the @@\frac{1}{2}n@@ for the midlines and edges of even length, giving @@n-1@@ colors total. Of course, I didn't realize this at the time. Instead, I tried to find a number theoretic approach to coloring the edges of even length, again to no avail. I only realized my geometric and number theoretic approaches could be combined when I saw some of the pretty pictures generated by the latter, such as the one below.
So then, my path was clear. I'd first recurse down to an odd multiple of two, then use my geometric approch to color all the midlines and edges of even length, and finally use my number theoretic approach to color the remaining edges. I wrote a Python program to do this and tested my algorithm all the way up to @@K_{500}@@. I also wrote some SageMath code to display the results. It's not efficient in the slightest, and it's not even the best algorithm to do this, but it gets the job done.
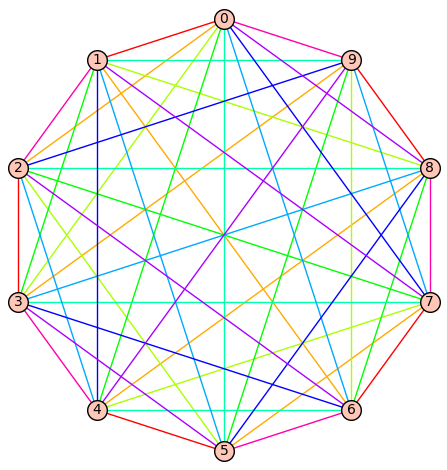
And so, I'd finished about a month of work. My last two posts have been quite long. I plan to only do that when it comes naturally, and not to force myself to wrote long-form content if I don't have any. Besides that, I enjoyed rediscovering this theorem, or rather a special case of it. I find solved problems a good source of puzzles. They're quite challenging, but still within the realm of a student's understanding. That's why I do them.
Resources