Some Intuition for Why the Cross Product Works

For some reason, the cross product has always been somewhat mysterious to me. At least, more so than the dot product. With the latter, there are many easy ways to at least gain some intuition for why it works — why perpendicular vectors have a dot product of zero. You could, for instance, consider planes in @@\mathbb{R}^n@@ (something like @@2x+3y+4z=0@@), then notice that changing the constant only changes placement and not slope, so it looks like the plane is being shifted along a vector perpendicular to it. You could also consider the gradient of a "linear" function like @@f(x,y) = 3x + 2y@@, seeing that the level surfaces are planes and that the gradient must necesarrily be perpendicular to level surfaces for the directional derivative to vanish.

This intuition is easy to come by for the dot product, but I've not seen the same for the cross product. In school, I was only taught its definition as %% \mathbf{u} \times \mathbf{v} = \det \begin{pmatrix} \hat{i} & \hat{j} & \hat{k} \nl & \mathbf{u} & \nl & \mathbf{v} & \end{pmatrix}, %% where we take @@\mathbf{u}@@ and @@\mathbf{v}@@ to be row vectors, and we abuse notation by treating the three basis vectors as elements in the matrix. It's not immediately clear what meaning this has, or why the cross product has the properties it does. It's not clear why @@\mathbf{u} \times \mathbf{v}@@ is orthogonal to both @@\mathbf{u}@@ and @@\mathbf{v}@@, or why the former's norm is equal to the area of the parallelogram "spanned" by the latter.

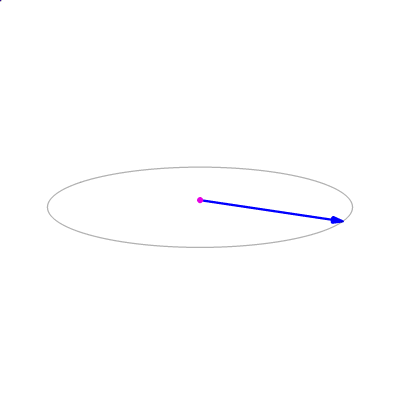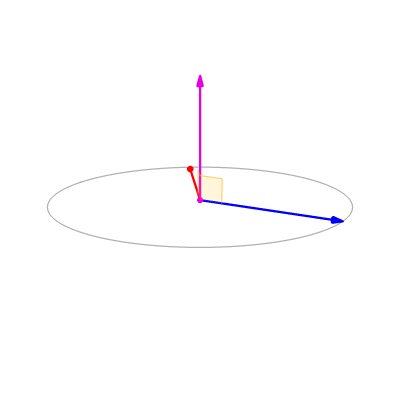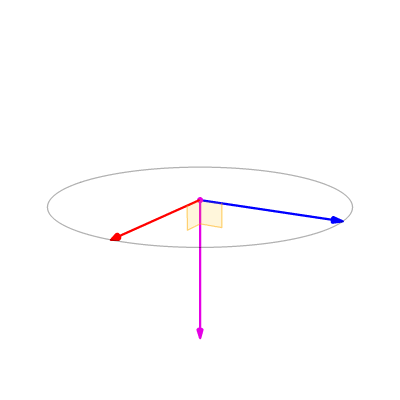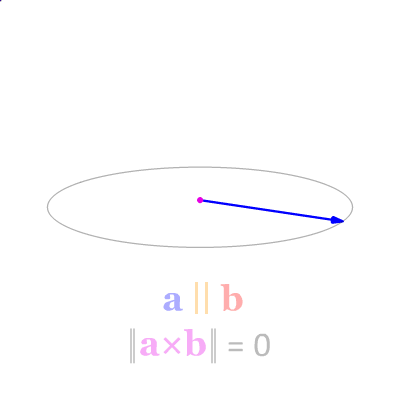
So let's try to build this from the ground up. What do we want the cross product to mean? We want to be able to measure how perpendicular two vectors (@@\mathbf{u}@@ and @@\mathbf{v}@@) are, and we can do this by using as a proxy the area of the parallelogram they span, as I think this GIF shows. Okay, how do we measure that area? A priori, I don't know how to measure areas in 3D space, but I do know how to measure volumes through the determinant. Perhaps we could pick an arbitrary test vector @@\mathbf{t}@@, then calculate @@\det\begin{pmatrix} \mathbf{u} & \mathbf{v} & \mathbf{t} \end{pmatrix}^\top@@. Given some details about @@\mathbf{t}@@, like how long it is and how much of it lies parallel to @@\mathbf{u}@@ and @@\mathbf{v}@@, we should be able to find the area we're after, as the image below makes clear. %% \det\begin{pmatrix}\mathbf{u}&\mathbf{v}&\mathbf{t}\end{pmatrix}^\top = Ah %%

You might notice something strange when doing the aforementioned computation, which becomes obvious when I fix @@\mathbf{u}@@ and @@\mathbf{v}@@ and let the test vector vary. Consider, for example, setting @@\mathbf{u} = \langle 1,2,3 \rangle@@ and @@\mathbf{v} = \langle 4,5,6 \rangle@@. We then compute %%\begin{align*} \det\begin{pmatrix}1&2&3\nl 4&5&6\nl &\mathbf{t}&\end{pmatrix} &= -3t_1 + 6t_2 - 3t_3 \nl &= \langle -3,6,-3 \rangle \cdot \mathbf{t}. \end{align*}%% The determinant on the LHS, which computes volumes, turns into a dot product on the RHS, which computes how parallel two vectors are! In general, we may write %% \det\begin{pmatrix}&\mathbf{u}&\nl&\mathbf{v}&\nl&\mathbf{t}&\end{pmatrix} = \mathbf{f}(\mathbf{u}, \mathbf{v}) \cdot \mathbf{t}, %% then start asking about the properties of @@\mathbf{f}@@. Letting @@\mathbf{t} = \mathbf{u}@@ or @@\mathbf{v}@@ shows that @@\mathbf{f}@@ is always orthogonal to its arguments since the determinant on the LHS clearly goes to zero in that case. Furthermore, as shown in the previous figure, letting @@\mathbf{t} = \mathbf{f}@@ itself allows us to express the volume on the right hand side as the area @@A@@ of the base spanned by @@\mathbf{u}@@ and @@\mathbf{v}@@ times the height of the parallelapiped, which is just @@||\mathbf{f}||@@ since it's orthogonal to it's arguments. Thus %%\begin{align*} A\,||\mathbf{f}(\mathbf{u},\mathbf{v})|| &= ||\mathbf{f}(\mathbf{u},\mathbf{v})||^2 \nl A &= ||\mathbf{f}(\mathbf{u},\mathbf{v})||. \end{align*}%% Finally, since the valueof @@\mathbf{f}@@ is tied to the determinant its computed from, we'd expect it to inherit some of its properties, like multi-linearity and vanishing on a zero argument or on linearly dependent input vectors.

Obviously, @@\mathbf{f}(\mathbf{u},\mathbf{v}) = \mathbf{u} \times \mathbf{v}@@ in three dimensions, but none of what I've said here is restricted to @@\mathbb{R}^3@@. We could make a "cross product" for higher dimensions, defined as a multilinear function from @@(\mathbb{R}^n)^{n-1} \to \mathbb{R}^n@@ satisfying %% \det\begin{pmatrix}&\mathbf{v}_1&\nl&\mathbf{v}_2&\nl&\vdots&\nl&\mathbf{v}_{n-1}&\nl&\mathbf{t}&\end{pmatrix} = \mathbf{f} \cdot \mathbf{t}.%% It would also satisfy the nice properties we outlined earlier — it'd be orthogonal to its arguments and have its length represent the @@n-1@@ dimensional area of the hyper-parallelapiped spanned by its input vectors. Indeed, it would agree with how we'd naturally extend the "standard" definition, with the only difference being a negative sign in even dimensions. Furthermore, it should be possible to generalize to two test vectors, or three, or more, though I don't know how exactly. Probably something to do with tensors.

Either way, I hope this sheds some light on why the cross product is defined the way it is. Yes, it just shows the same thing in a different way, but being able to see these different views is a good step toward understanding, isn't it?